8. Rozkłady Chi kwadrat t-Studenta, i F-Snedecora.

Do testów statystycznych przydatne są rozkłady t-Studenta, Chi kwadrat i F-Snedecora.

Rozkładów tych jest nieskończenie wiele ale są ponumerowane. Kolejny numer nosi nazwę liczby stopni swobody.

Rozkład Chi kwadrat o n stopniach swobody to suma kwadratów n niezależnych zmiennych losowych, z których każda ma rozkład normalny standardowy.

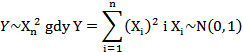
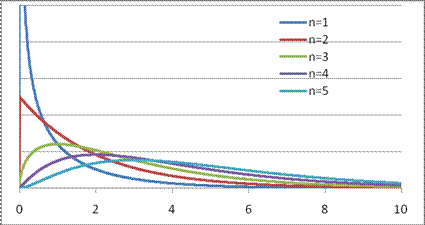
Wykres przedstawia gęstości zmiennych losowych o rozkładach chi kwadrat o różnych liczbach stopni swobody.

Rozkład t-Studenta o n stopniach swobody jest rozkładem ciągłym takim, że

gdzie U jest zmienną losową o rozkładzie normalnym standardowym a Z jest zmienną losową o rozkładzie chi kwadrat o n stopniach swobody i zmienne te są niezależne.

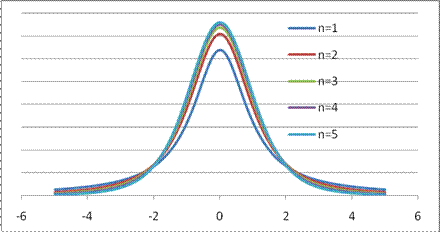
Wykres przedstawia gęstości zmiennych losowych o rozkładach t-Studenta o różnych liczbach stopni swobody.

Rozkłady F-Snedecora są ponumerowane dwiema liczbami stopni swobody.
Jeżeli zmienna losowa X ma rozkład chi kwadrat o n stopniach swobody a niezależna od niej zmienna losowa Y ma rozkład chi kwadrat o m stopniach swobody to zmienna

ma rozkład F-Snedecora o n, m stopni swobody.

W zapisie formalnym: _.